Multi-Objective Multi-Modal Optimization
Multi-objective Optimization Problems (MOPs) have typically several conflicting objectives which are supposed to be optimized at the same time. The solution of such problems is a set of so-called Pareto-optimal solutions. In our research in the area of Multi-Modal Multi-Objective Optimization we work on a particular sort of MOPs, namely Multi-Modal problems, which are present in many real-world problems. In such Multi-Modal problems, multiple equivalent solutions map to the same Pareto-optimal solution. The major challenge for the optimization algorithms is to discover these several equivalent solutions in the decision space. In our research we work on a variety of approaches to address this issue. In one of our recent works, we propose a new algorithm NxEMMO which enforces the diversity of the solutions in decision-space:
- Mahrokh Javadi and Sanaz Mostaghim
- Using neighborhood-based Density Measures for Multimodal Multi-Objective Optimization
- Accepted at the 11th International Conference on Evolutionary Multi-Criterion Optimization (EMO 2021), Shenzhen, China, 2021
In the following videos, the evolution of the population is shown in the search space for NxEMMO (left videos) and NSGA-II (right videos) as a baseline algorithms. The obtained solutions are shown as red stars, and the blue lines indicate the true Pareto-optimal solutions.
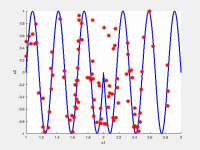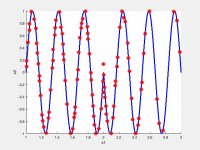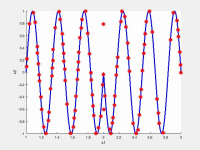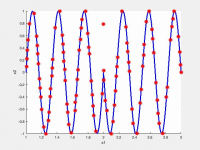
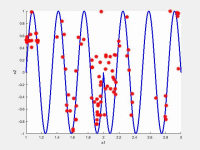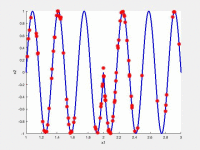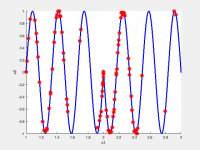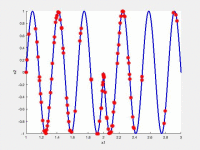
NxEMMO (left), NSGA-II (right)
Decision space for MMF1 test problem
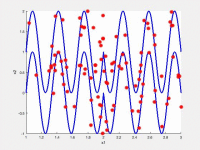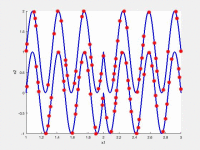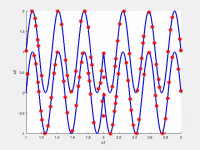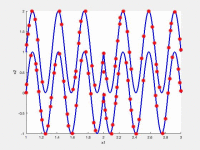
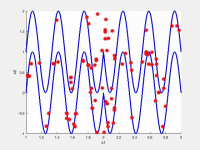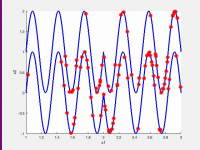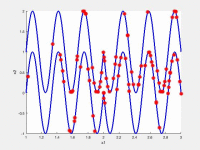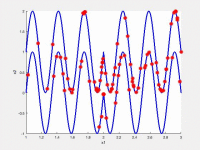
NxEMMO (left), NSGA-II (right)
Decision space for MMF6 test problem
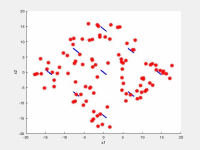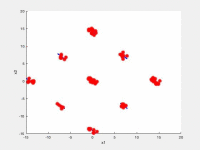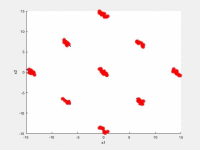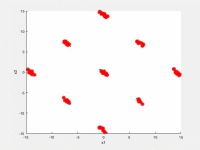
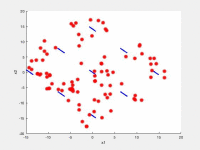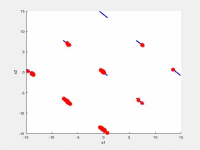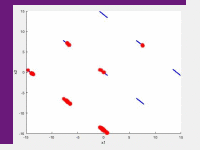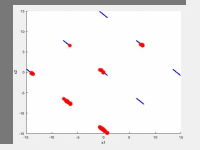
NxEMMO (left), NSGA-II (right)
Decision space for SYM-PART-Rotated test problem